Welcome to pyrodeo!¶
Pyrodeo is a Python implementation of RODEO (ROe solver for Disc-Embedded Objects), a Roe solver implementation aimed at hydrodynamic simulations of astrophysical discs.
Installation¶
If Python is not installed, download from here and install. The latest versions of Python come with package manager pip included. Then Pyrodeo can be installed from the command line simply by entering:
pip install pyrodeo
Quick start¶
Within Python, first import the simulation module:
>>> import pyrodeo
Create a simulation in Cartesian geometry with standard parameters:
>>> sim = pyrodeo.Simulation.from_geom('cart')
Run the simulation up to t=0.25:
>>> sim.evolve([0.25])
Since the standard initial conditions consist of constant density and pressure and zero velocity, no visible evolution takes place. For more interesting examples, see Examples.
Equations solved¶
The current version supports inviscid isothermal hydrodynamics in three spatial
dimensions. Isothermal means the pressure 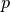 is related to the
density
is related to the
density 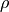 simply through
simply through 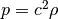 , where the sound
speed
, where the sound
speed  is either a constant (fully isothermal) or a
prescribed function of position (locally isothermal). Four geometries
are available: Cartesian coordinates, the shearing sheet, cylindrical
coordinates and spherical coordinates.
is either a constant (fully isothermal) or a
prescribed function of position (locally isothermal). Four geometries
are available: Cartesian coordinates, the shearing sheet, cylindrical
coordinates and spherical coordinates.
Cartesian coordinates¶
In Cartesian coordinates, we have the continuity equation:
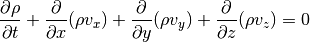
Momentum in x-direction:
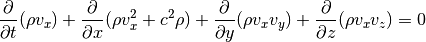
Momentum in y-direction:
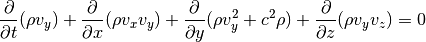
Momentum in z-direction:
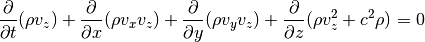
Shearing Sheet¶
The Shearing Sheet is essentially a Cartesian model of a small patch
in an astrophysical disc. This patch is rotating at the local
Keplerian angular velocity 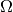 , which means that Coriolis
and centrifugal-type forces need to be included on the right-hand side
of the equations. On the other hand, the patch is assumed to be small
enough so that a local Cartesian frame can be used in stead of
cylindrical coordinates. Usually the computational domain is taken to
be periodic in y and shear-periodic in x (periodic but corrected for
the shear). We therefore still have the continuity equation:
, which means that Coriolis
and centrifugal-type forces need to be included on the right-hand side
of the equations. On the other hand, the patch is assumed to be small
enough so that a local Cartesian frame can be used in stead of
cylindrical coordinates. Usually the computational domain is taken to
be periodic in y and shear-periodic in x (periodic but corrected for
the shear). We therefore still have the continuity equation:
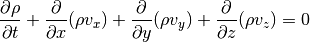
The x-momentum equation now includes source terms on the right-hand side:
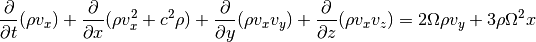
Same for the momentum equation in y-direction:
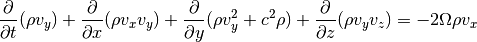
In the z-direction we get a source term due to the vertical component of the stellar gravity:
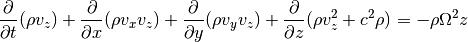
Note
In the shearing sheet the sound speed should really be constant (no
locally isothermal shearing sheet). Together, sound speed and
angular velocity define a length scale 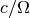 , which is a
measure of the scale height of the disc. Typically one chooses
, which is a
measure of the scale height of the disc. Typically one chooses
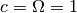 , so that distances are measured in scale heights
and time in inverse orbital frequency.
, so that distances are measured in scale heights
and time in inverse orbital frequency.
Cylindrical coordinates¶
For a full disc in two dimensions cylindrical coordinates
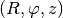 are preferred. This time we have geometrical
source terms and gravity from the central object to worry about. The
continuity equation now reads:
are preferred. This time we have geometrical
source terms and gravity from the central object to worry about. The
continuity equation now reads:
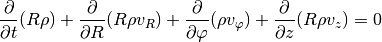
The radial momentum equation now includes source terms representing centrifugal and gravitational forces, in addition to a geometrical pressure source term:
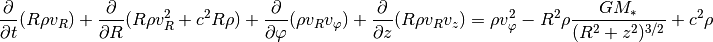
In the 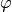 direction we get a Coriolis source term:
direction we get a Coriolis source term:
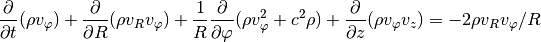
In the vertical direction we again have the vertical component of the stellar gravity:
Note
The unit of mass is taken to be the mass of the central object. The
unit of distance is some reference radius. The unit of time is the
inverse angular velocity at the reference radius. In this system of
units, the gravitational constant is unity, and one orbit equals
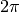 time units.
time units.
Spherical coordinates¶
For a full disc in three dimensions spherical coordinates
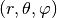 are often preferred. The continuity and
momentum equations now read:
are often preferred. The continuity and
momentum equations now read:
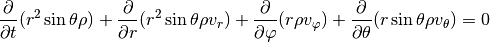
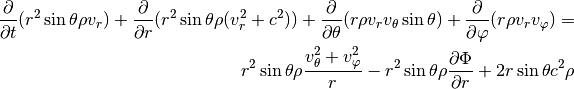
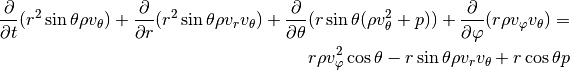
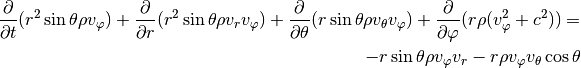
Extra source terms¶
Pyrodeo solves inviscid isothermal hydrodynamics, and in the shearing sheet and cylindrical and spherical geometries only gravity from the central object is considered. Extra physics, as far as it concerns extra source terms, can be added by a user-defined source integration function. See the Examples section. This function is called once per time step and can also be used for monitoring various quantities (mass, torque on planet, etc.).
Numerical method¶
Dimensional splitting¶
Pyrodeo uses dimensional splitting to integrate the equations.
First direction (x, R, r)¶
For the x direction (therefore neglecting y- and z-derivatives), we can cast the equations into the following form:
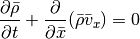
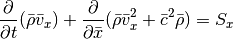
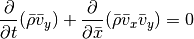
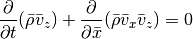
For the Cartesian setup, we simply have
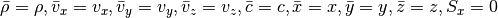
For the shearing sheet, we need
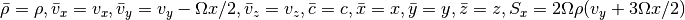
In cylindrical coordinates we need
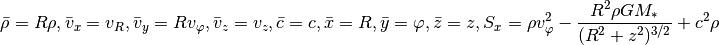
Finally, for spherical coordinates we need:
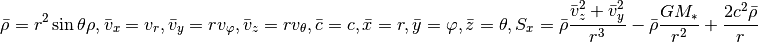
Second direction (y, 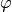 )¶
)¶
For the y-integration (neglecting x- and z-derivatives) we can cast the equations in the form:
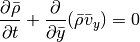
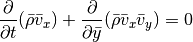
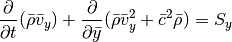
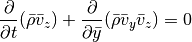
For both the Cartesian setup and the shearing sheet, we simply have
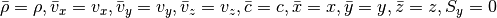
In cylindrical coordinates we need
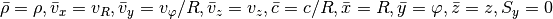
Finally, spherical coordinates:
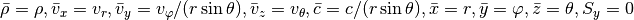
Third direction (z, 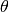 )¶
)¶
Finally, for the z integration we can cast the equations in the form:
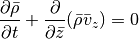
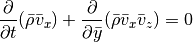
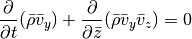
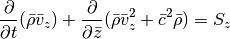
For both the Cartesian setup, we simply have
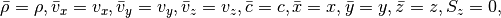
with the shearing sheet being exactly the same but with a non-zero
source 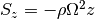 .
.
In cylindrical coordinates we need
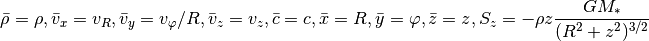
Finally, spherical coordinates:
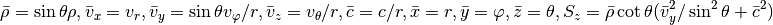
Unified approach¶
Note that the resulting equations are very symmetric in x, y and z: if we swap x and y in the y integration the equations have exactly the same form as for the x integration. Similar for the z integration when swapping z and x. Therefore, if we prepare all quantities appropriately, we only need a single hydrodynamic solver that is able to advance the system
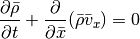
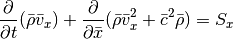
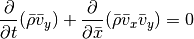
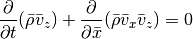
This is what is done in the Roe class. The necessary
preparation is done in the Hydro class.
Orbital advection¶
In the case of the shearing sheet and the cylindrical disc there is a
large 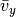 that severely limits the time step. This limit
can be overcome by splitting the y integration one more by writing
that severely limits the time step. This limit
can be overcome by splitting the y integration one more by writing
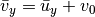 where
where 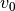 is independent of y
is independent of y
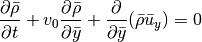
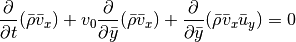
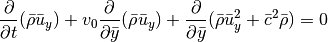
The terms involving 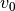 make up a linear advection problem
that can be solved straightforwardly for any time step. This is done
in the
make up a linear advection problem
that can be solved straightforwardly for any time step. This is done
in the LinearAdvection class. The remaining terms are
integrated in the Roe class, but at a much larger time step
because presumably  .
.
Algorithm overview¶
A single time step in Hydro.evolve consists of the following steps:
- Calculate time step using
Hydro.calc_time_step. - Set shear periodic boundary conditions if necessary.
- Preprocessing step to cast the equations in the same form for all
geometries and directions, while at the same time calculating the
source term using
Hydro.preprocess. - Use the Roe solver to advance the hydrodynamic equations using
Roe.step. - Do orbital advection if necessary using
Hydro.orbital_advection. - Do the inverse of step 3, getting all quantities back to their
original form in
Hydro.postprocess. - Integrate any extra source terms.
Boundary conditions¶
The available boundary conditions are
- ‘closed’: closed boundary, i.e. no mass flow through the boundary. Waves will be reflected off the boundary.
- ‘periodic’: periodic boundary.
- ‘nonreflecting’: allow waves to pass through unhindered.
- ‘symmetric’: assume boundary is a symmetry plane. Very much like a closed boundary, but less general in that it needs the boundary to be a plane of symmetry.
By default, all boundaries are set to be closed; this can be changed
by changing the boundaries attribute of the Param class.
Output¶
Once the integration routine Simulation.evolve has finished the final state
is available through simulation.state(). In addition, an output
file rodeo.h5 is created containing the state at all specified
checkpoints. This is an HDF5 file
created with h5py. It contains the
following groups:
- param: Simulation parameters as specified in the
Paramclass. - coords: Coordinates from the
Coordinatesclass. - checkpoint#: State at checkpoint, where # stands for an integer.
Note
Both state and coordinate arrays include two ghost zones on each side in all directions. This is in order to be able to restore a simulation from a checkpoint.
Note
The value stored in state.vely is the y-velocity with the orbital advection velocity removed! In other words, the equilibrium solution in a constant pressure shearing sheet or cylindrical disc has vanishing state.vely.
An example of reading the file and plotting using matplotlib:
#!/usr/bin/python
import numpy as np
import matplotlib.pyplot as plt
import h5py
with h5py.File('./rodeo.h5', "r") as hf:
# Select last available checkpoint
last_checkpoint = None
for k in hf.keys():
if (k != 'coords' and k != 'param'):
last_checkpoint = k
# Get x coordinate
gc = hf.get('coords')
x = np.array(gc.get('x'))
# Get density
g = hf.get(last_checkpoint)
dens = np.array(g.get('dens'))
# Simulation time at checkpoint
t = g.attrs['time']
print('Plotting ' + last_checkpoint + ' at t = {}'.format(t))
plt.plot(x[:,0], np.mean(dens, axis=1))
plt.show()
Examples¶
Shock tube¶
A simple example in Cartesian geometry is a one-dimensional isothermal shock tube:
#!/usr/bin/python
import numpy as np
import matplotlib.pyplot as plt
import pyrodeo
# Create simulation with default resolution and domain
sim = pyrodeo.Simulation.from_geom('cart')
# The basic state will have density and sound speed unity everywhere,
# and the velocity will be zero. In order to create a simple shock tube,
# now set density to 1/10 for x > 0.
sel = np.where(sim.coords.x > 0.0)
sim.state.dens[sel] = 0.1
# Evolve until t = 0.25
sim.evolve([0.25], new_file=True)
# Plot results
plt.plot(sim.coords.x[:,0,0], sim.state.dens[:,0,0])
plt.show()
The standard grid dimensions are (100,1), which means 100 cells in x
and 1 in y. Try a higher resolution by explicitly specifying the dimensions in
Simulation.from_geom.
Instability in shearing sheet¶
A more demanding two-dimensional calculation involves the instability of a sharp density ridge in the shearing sheet:
#!/usr/bin/python
import numpy as np
import pyrodeo
# Domain half-width in x and y
Lx = 2.0
Ly = 20.0
# Create simulation, setting grid dimensions and domain
sim = pyrodeo.Simulation.from_geom('sheet',
dimensions=[32, 64, 1],
domain=([-Lx, Lx], [-Ly, Ly], []))
sim.param.boundaries[0] = ['shear periodic','shear periodic']
sim.param.boundaries[1] = ['periodic','periodic']
# Density profile: single maximum in middle of domain
sim.state.dens = 0.5*np.cos(np.pi*sim.coords.x/Lx) + 1.0
# Equilibrium vy to compensate for pressure gradient
sim.state.vely = -0.25*np.pi*np.sin(np.pi*sim.coords.x/Lx)/(sim.state.dens*Lx)
# Add some noise to seed instability
sim.state.dens += 0.01*np.random.random_sample(np.shape(sim.state.dens))
# Evolve until t = 100.0
sim.evolve(0.25*np.arange(400), new_file=True)
The checkpoints have been chosen close enough together to allow for the results to be animated:
#!/usr/bin/python
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import h5py
# Return density at checkpoint n
def density_at_checkpoint(file_name, n):
dens = None
with h5py.File(file_name, 'r') as hf:
maxn = len(hf.keys()) - 2
if n >= maxn:
n = maxn - 1
s = "checkpoint{}".format(n)
g = hf.get(s)
dens = np.array(g.get('dens'))
return dens
fig = plt.figure()
# Show initial conditions (checkpoint 0)
file_name = './rodeo.h5'
dens = density_at_checkpoint(file_name, 0)
im = plt.imshow(dens[:,:,0], animated=True)
# Get next checkpoint
n = 0
def updatefig(*args):
global n
dens = density_at_checkpoint(file_name, n)
im.set_array(dens[:,:,0])
n += 1
return im,
# Animate!
ani = animation.FuncAnimation(fig, updatefig, interval=50, blit=True)
plt.show()
Disc-planet interaction¶
As the final, most complex example, consider a planet embedded in a disc in cylindrical coordinates. Since pyrodeo only includes gravity from the central star, we need to provide an extra source term to account for the gravitational force due to the planet. In addition, we define wave-killing zones on the radial edges of the domain to avoid wave reflection. It will take some time to run this simulation, so have a cup of tea and come back to see a Jupiter-like planet carve out a gap in the disc.
#!/usr/bin/python
import numpy as np
import pyrodeo
# Extra source terms: planet gravity
def planet_source(t, dt, coords, state, planetParam):
# Mass ratio planet/star
mp = planetParam[0]
# Softening length planet potential
eps = planetParam[1]
# Coordinates
r = coords.x
p = coords.y
# Planet coordinates
rp = 1.0
pp = 0.0
# Distance to the planet
dist = np.sqrt(r*r + rp*rp - 2.0*r*rp*np.cos(p - pp) + eps*eps)
# Potential gradient
dpotdr = mp*(r - rp*np.cos(p - pp))/(dist*dist*dist)
dpotdp = mp*r*rp*np.sin(p - pp)/(dist*dist*dist)
# Indirect term
dpotdr += mp*np.cos(p - pp)/(rp*rp)
dpotdp -= mp*r*np.sin(p - pp)/(rp*rp)
# Resulting source term
source_velx = -dpotdr
source_vely = -dpotdp/(r*r)
# Damping boundary conditions
Rin = 100.0*(r - 0.5)*(r - 0.5)
Rin[np.where(r > 0.5)] = 0.0
Rout = (r - 2.1)*(r - 2.1)/(0.4*0.4)
Rout[np.where(r < 2.1)] = 0.0
R = (Rin + Rout)*np.power(r, -1.5)
# Damp towards initial state
source_dens = -(state.dens - 1.0)*R
source_velx -= state.velx*R
source_vely -= state.vely*R
# Integrate extra source terms
state.dens += dt*source_dens*state.no_ghost
state.velx += dt*source_velx*state.no_ghost
state.vely += dt*source_vely*state.no_ghost
sim = pyrodeo.Simulation.from_geom('cyl',
dimensions=[128, 384, 1],
domain=([0.4, 2.5], [-np.pi, np.pi], []))
# Sound speed constant H/r = 0.05
sim.state.soundspeed = 0.05*sim.state.soundspeed/np.sqrt(sim.coords.x)
sim.param.boundaries[0] = ['closed','closed']
sim.param.boundaries[1] = ['periodic','periodic']
# Simulate a Jupiter planet up to 100 orbits
sim.evolve(2.0*np.pi*np.array([1.0,2.0,5.0,10.0,20.0,50.0,100.0]),
planet_source, (0.001, 0.6*0.05), new_file=True)
Class reference¶
Coordinates¶
Coordinate class used in pyrodeo.
The Coordinate class hold the x, y and z coordinates as 3D ndarrays. In addition, it holds the step size in x, y and z and the size of the grid in x, y and z.
-
class
pyrodeo.coords.Coordinates(x, y, z, log_radial=False)[source]¶ Class containing coordinates used in pyrodeo.
Parameters: - x (ndarray) – 2D ndarray containing x coordinates
- y (ndarray) – 2D ndarray containing y coordinates
- z (ndarray) – 2D ndarray containing z coordinates
- log_radial (
bool, optional) – Flag whether x is a logarithmic radial coordinate.
Note
The validity of the arrays is not checked! To be used in a simulation, they should have the same shape, with x[:,j,k] containing the x coordinates for all j,k, y[i,:,k] containing the y coordinates for all i,k and z[i,j,:] containing the z coordinates for all i,j. In addition, x, y and z should have a constant step size.
The following public attributes are available:
-
x¶ ndarray – 2D ndarray containing x coordinates
-
y¶ ndarray – 2D ndarray containing y coordinates
-
z¶ ndarray – 3D ndarray containing z coordinates
-
dimensions¶ [int, int, int] – grid dimensions in the x, y and z direction
-
dxyz¶ [float, float, float] – step size in the x, y and z direction
-
log_radial¶ bool, optional – Flag whether x is a logarithmic radial coordinate.
-
classmethod
from_1d(x, y, z, log_radial=False)[source]¶ Initialize from 1D arrays.
Build coordinates from existing 1D ndarrays (should include ghost cells). Calculate dimensions and step sizes.
Parameters: - x (ndarray) – 1D ndarray containing x coordinates
- y (ndarray) – 1D ndarray containing y coordinates
- z (ndarray) – 1D ndarray containing z coordinates
- log_radial (
bool, optional) – Flag whether x is a logarithmic radial coordinate.
Note
The validity of arrays x, y and z is not checked. They should have constant step size.
-
classmethod
from_dims(dimensions=(100, 1, 1), domain=([-0.5, 0.5], [], []), log_radial=False)[source]¶ Initialize from dimensions and domain size.
Build coordinates given the dimensions of the grid and the size of the domain. Some basic checks are performed to ensure the resulting coordinates are valid.
Parameters: - dimensions (
(int,int,int), optional) – Dimensions of the grid - domain (
([float,float],[float,float],[float,float]), optional) – Domain boundaries in x, y and z - log_radial (
bool, optional) – Flag whether x will be a logarithmic radial coordinate.
- dimensions (
State¶
Definition of State class used in pyrodeo.
The State class holds density, velocity and sound speed for a pyrodeo simulation
-
class
pyrodeo.state.State(dens, velx, vely, velz, soundspeed)[source]¶ Construct state holding density, velocity and sound speed for a pyrodeo simulation.
Parameters: - dens (ndarray) – 3D ndarray containing density.
- velx (ndarray) – 3D ndarray containing x velocity.
- vely (ndarray) – 3D ndarray containing y velocity.
- velz (ndarray) – 3D ndarray containing z velocity.
- soundspeed (ndarray) – 3D ndarray containing sound speed.
Note
No checks are performed whether density, velocity and sound speed are valid arrays. They should all have the same shape, the same as the arrays of
Coordinates.The following public attributes are available:
-
dens¶ ndarray – 3D ndarray containing density.
-
velx¶ ndarray – 3D ndarray containing x velocity.
-
vely¶ ndarray – 3D ndarray containing y velocity.
-
velz¶ ndarray – 3D ndarray containing z velocity.
-
soundspeed¶ ndarray – 3D ndarray containing sound speed.
-
no_ghost¶ ndarray – 3D ndarray flagging whether a cell is a ghost cell (=0) or an internal cell (=1)
-
classmethod
copy(other_state)[source]¶ Construct state from other State.
Set this instance of State equal to an other State, performing an explicit copy.
Parameters: other_state (State) – State from which to copy.
Param¶
Simulation parameters used in pyrodeo.
The Param class holds parameters necessary for a pyrodeo simulation.
-
class
pyrodeo.param.Param(param_list)[source]¶ Create instance from list of parameters.
Parameters: param_list ([str, float, float, float, str, str, str]) – List of parameters; geometry (string), courant (float), fluxlimiter (float), frame_rotation (float), log_radial (bool), boundaries x in (string), boundaries x out (string), boundaries y in (string), boundaries y out (string), boundaries z in (string) and boundaries z out (string) Note
The validity of the parameters is not checked.
The following public attributes are available:
-
geometry¶ string – ‘cart’ (Cartesian coordinates), ‘sheet’ (shearing sheet), ‘cyl’ (cylindrical coordinates) or ‘sph’ (spherical coordinates).
-
courant¶ float – Courant number, should be > 0 and < 1.
-
limiter_param¶ float – Limiter parameter. Should be between 1 (minmod) and 2 (superbee).
-
min_dens¶ float – Minimum density to switch to HLL solver to remain positive.
-
frame_rotation¶ float – Frame rotation rate. Ignored in Cartesian coordinates, should be unity in a shearing sheet calculation and corresponds to the angular velocity of the coordinate frame in cylindrical coordinates.
-
log_radial¶ bool – Flag whether to use logarithmic radial coordinates in cylindrical geometry.
-
boundaries¶ (str,str), (str,str), (str,str) – Boundary conditions (in and out) in x y and z: ‘nonreflecting’, ‘closed’, ‘symmetric’, or ‘periodic’. In shearing sheet mode, the x boundary can be ‘shear periodic’.
-
classmethod
from_geom(geometry, log_radial=False, boundaries=[['closed', 'closed'], ['closed', 'closed'], ['closed', 'closed']])[source]¶ Initialization from geometry and boundary conditions.
Construct Parameter object from geometry and boundary conditions. All other parameters are set to standard values. Check if geometry and boundary conditions are valid.
Parameters: - geometry (string) – ‘cart’ (Cartesian coordinates), ‘sheet’ (shearing sheet), ‘cyl’ (cylindrical coordinates) or ‘sph’ (spherical coordinates).
- boundaries ((str,str), (str,str), (str,str)) – boundary conditions; ‘closed’, ‘nonreflecting’, ‘symmetric’, or ‘periodic’. In shearing sheet mode, the x boundary can be ‘shear periodic’.
-
Conservation law solver¶
Defines a generic conservation law solver.
-
class
pyrodeo.claw_solver.ClawSolver[source]¶ Generic conservation law solver.
Note
Serves as a base class to construct various solvers. Can not be used on its own.
The following method is available:
-
limiter(a, b, sb)[source]¶ Limiter function to limit slopes/fluxes.
This limiter function can, based on the parameter sb, emulate total variation diminishing limiters from minmod (sb = 1) to superbee (sb = 2).
Parameters: - a (ndarray) – First slope to compare.
- b (ndarray) – Second slope to compare.
- sb (float) – Limiter parameter. Should be >= 1 (minmod, most diffusive limiter) and <= 2 (superbee, least diffusive limiter).
Returns: Limited slopes.
Return type: ndarray
-
Linear advection solver¶
Defines a linear advection solver in a periodic domain.
-
class
pyrodeo.linear_advection.LinearAdvection(advection_velocity, limiter_parameter)[source]¶ Linear advection solver in periodic domain.
Parameters: - advection_velocity (ndarray) – Advection velocity. Must have the same shape as
Statemembers (density, velocity) to be advected and must be uniform in the first dimension (x). - limiter_parameter (float) – Parameter setting the limiter function. Should be >= 1 (minmod limiter, most diffusive) and <= 2 (superbee limiter, least diffusive).
Note
The linear advection equation is solved on a periodic x domain. The advection velocity can not depend on x. If advecting over y, the state will have to be transposed first.
The following public attributes and methods are available:
-
advection_velocity¶ ndarray – Advection velocity. Must have the same shape as
Statemembers (density, velocity) to be advected and must be uniform in the first dimension (x).
-
sb¶ float – Parameter setting the limiter function. Should be >= 1 (minmod limiter, most diffusive) and <= 2 (superbee limiter, least diffusive).
- advection_velocity (ndarray) – Advection velocity. Must have the same shape as
Roe solver¶
Defines the Roe class defining the Roe solver.
-
class
pyrodeo.roe.Roe(flux_limiter, min_dens)[source]¶ Construct class for the Roe solver.
Constructor sets two basic attributes (sb and min_dens), after which a time step can be taken through the
step()method.Parameters: - flux_limiter (float) – Flux limiter parameter. Should be >= 1 (minmod, most diffusive limiter) and <= 2 (superbee, least diffusive limiter).
- min_dens (float) – Minimum density when to switch to HLL to preserve positivity.
The following attributes and methods are available:
-
sb¶ float – Flux limiter parameter. Should be >= 1 (minmod, most diffusive limiter) and <= 2 (superbee, least diffusive limiter).
-
min_dens¶ float – Minimum density when to switch to HLL to preserve positivity.
-
limit_flux(dens, dens_left, f1dens, f2dens, dtdx)[source]¶ Limit second order flux to preserve positivity
Calculate the maximum contribution of the second order flux in order for the density to remain positive.
Parameters: - dens (ndarray) – Current density.
- dens_left (ndarray) – Density in the cell to the left
- f1dens (ndarray) – First order mass flux.
- f2dens (ndarray) – Second order mass flux.
- dtdx (float) – Time step / space step
Returns: Array with values >= 0 and <= 1 specifying the maximum contribution of second order flux for the density to remain positive.
Return type: ndarray
-
step(dt, dx, state, source, bc)[source]¶ Update state for a single time step.
Parameters: - dt (float) – Time step.
- dx (float) – Space step.
- state (
State) – CurrentState, will be updated. - source (ndarray) – Geometric source terms, must have same shape as state.dens.
- bc (str, str) – Boundary conditions (in and out): ‘periodic’, ‘symmetric’, or ‘closed’ (other boundary conditions are dealt with elsewhere).
Hydro¶
Defines the Hydro class performing hydrodynamic updates of the state.
-
class
pyrodeo.hydro.Hydro(param, coords)[source]¶ Construct class for hydrodynamic updates.
Construct from existing instances of
ParamandCoordinates. It constructs aLinearAdvectioninstance which will deal with orbital advection, and aRoeinstance dealing with hydrodynamics of residual velocities.Parameters: - param (
Param) – Valid Param object, containing simulation parameters. - coords (
Coordinates) – Valid Coordinates object, containing x, y and z coordinates. Used to calculate orbital advection velocity.
The following attributes and methods are available:
-
orbital_advection¶ LinearAdvection– Instance ofLinearAdvectionclass used to do orbital advection.
-
calc_time_step(geometry, coords, state, log_radial=False)[source]¶ Calculate time step obeying the CFL condition.
Parameters: - geometry (str) – ‘cart’, ‘sheet’ or ‘cyl’.
- coords (
Coordinates) – ValidCoordinatesobject, containing x, y and z coordinates. - state (
State) – ValidStateobject, containing density and velocity. - log_radial (
bool, optional) – Flag indicating whether a logarithmic radial coordinate is used
Returns: Maximum time step obeying the CFL condition.
Return type: float
-
evolve(t, t_max, coords, param, state, source_func, source_param)[source]¶ Evolve state from t to tmax.
Parameters: - t (float) – Current simulation time.
- t_max (float) – Simulation time to reach before stopping.
- coords (
Coordinates) – ValidCoordinatesobject, containing x and y coordinates. - param (
Param) – ValidParamobject, containing simulation parameters. - state (
State) – ValidStateobject, containing density and velocity. - source_func (callable) – Function integrating any extra source terms (non-geometric). It should accept the following arguments: t, dt, coords, state, source_param.
- source_param (array-like) – Extra parameters for source_func.
Returns: Tuple consisting of:
Return type: (tuple)
-
postprocess(coords, param, state, direction)[source]¶ Inverse of
preprocess().Reverse modifications by
preprocess().Parameters: - coords (
Coordinates) – ValidCoordinatesobject, containing x and y coordinates. - param (
Param) – ValidParamobject, containing simulation parameters. - state (
State) – ValidStateobject, containing density and velocity. - direction (int) – 0 (integrating x) or 1 (integrating y).
- coords (
-
preprocess(coords, param, state, direction)[source]¶ Modify state to quasi-cartesian form and calculate geometric source terms.
Isothermal hydrodynamics allows for a generic form of the equations in all geometries, subject only to modifications in the geometric source terms.
Parameters: - coords (
Coordinates) – ValidCoordinatesobject, containing x and y coordinates. - param (
Param) – ValidParamobject, containing simulation parameters. - state (
State) – ValidStateobject, containing density and velocity. - direction (int) – 0 (integrating x) or 1 (integrating y).
Returns: Geometric source term of the same shape as state.dens.
Return type: ndarray
- coords (
-
shear_periodic_boundaries(t, coords, state)[source]¶ Set shear-periodic boundary conditions.
In the shearing sheet geometry, the x direction can be quasi-periodic, i.e. periodic but modified for the shear. Imagine neighbouring sheets shearing past the center sheet.
Parameters: - t (float) – Current simulation time. Used to calculate over what distance neighbouring sheets have shifted since t = 0.
- coords (
Coordinates) – ValidCoordinatesobject, containing x and y coordinates. - state (
State) – ValidStateobject, containing density and velocity.
- param (
Simulation¶
Defines the Simulation class holding a pyrodeo simulation
-
class
pyrodeo.simulation.Simulation(param, coords, state, t, direc='./')[source]¶ Construct pyrodeo simulation.
Construct simulation from existing instances of
Param,CoordinatesandStateand given simulation time.Parameters: - param (
Param) – Valid Param object, containing simulation parameters. - coords (
Coordinates) – Valid Coordinates object, containing x, y and z coordinates - state (
State) – Valid State object, containing current density, velocity and sound speed. - t (float) – Simulation time.
- direc (
str, optional) – Output directory.
Note
While it is possible to set up a simulation using the basic constructor, no checks are performed whether the instances of
Param,CoordinatesandStateare valid. It is safer to usefrom_geom()which will set up the necessary valid instances.The following attributes and methods are available:
-
coords¶ Coordinates– Coordinates object holding x, y and z coordinates.
-
t¶ float – Current simulation time.
-
direc¶ string – Output directory.
-
checkpoint(new_file=False)[source]¶ Save checkpoint in ‘rodeo.h5’
Parameters: new_file ( bool,optional) – If true, create new output file ‘rodeo.h5’, otherwise append to file if it exists.
-
evolve(checkpoints, source_func=None, source_param=None, new_file=False)[source]¶ Evolve simulation over a list of checkpoints.
Parameters: - checkpoints (ndarray) – List of times to save checkpoints.
- source_func (
callable, optional) – Integrate extra source terms. Must be of the form f(t, dt, coords, state, source_param). - source_param (
ndarray, optional) – Parameters for extra source term. Will be passed to source_func. - new_file (
bool,optional) – If true, create new output file ‘rodeo.h5’, otherwise append to file if it exists.
-
classmethod
from_checkpoint(direc, n=None)[source]¶ Constructor for simulation class from checkpoint.
Construct simulation class from previously saved checkpoint.
Parameters: - direc (str) – Path to ‘rodeo.h5’. This will be the output directory as well.
- n (
int,optional) – Index of checkpoint to restore. If left None, restore last saved checkpoint.
-
classmethod
from_geom(geometry, dimensions=(100, 1, 1), domain=([-0.5, 0.5], [], []), log_radial=False, direc='./')[source]¶ Construct simulation from geometry.
Construct simulation class from geometry, grid dimensions and domain size. All other parameters will be set to defaults. Simulation time is set to zero.
Parameters: - geometry (string) – ‘cart’ (Cartesian coordinates), ‘sheet’ (shearing sheet), ‘cyl’ (cylindrical coordinates) or ‘sph’ (spherical coordinates).
- dimensions (
(int,int,int),optional) – Grid dimensions in x, y and z. - domain (
[(float,float),(float,float),(float,float)],optional) – Domain boundaries in x, y and z. - log_radial (bool) – Flag whether to use logarithmic radial coordinate
- direc (
str,optional) – Output directory, defaults to current directory.
- param (